实验室本科生在SCI期刊上发表气候变量降尺度校正的论文

在全球变化的背景下，青藏高原的气候也经历了前所未有的变化。GCM是预测全球尺度未来气候变化的重要手段，但GCM具有较粗的分辨率。当我们需要在站点尺度进行未来气候变化研究时，往往需要根据GCM或者区域气候模式（RCM）预测结果建立站点气候变量的未来趋势。已有研究已经建立了很多基于统计关系的方法，用以将粗分辨率模式模拟结果校正到站点尺度，其中一种广泛应用的方法是Quantile-Quantile (Q-Q)方法。本文为证实Q-Q方法在青藏高原上的适用性，利用36个站点，结合两个GCM（EC-Earth 3和MPI-ESM1.2-HR），在五个逐月变量（降水、气温、相对湿度、风速、气压）上对Q-Q方法进行综合的评估。

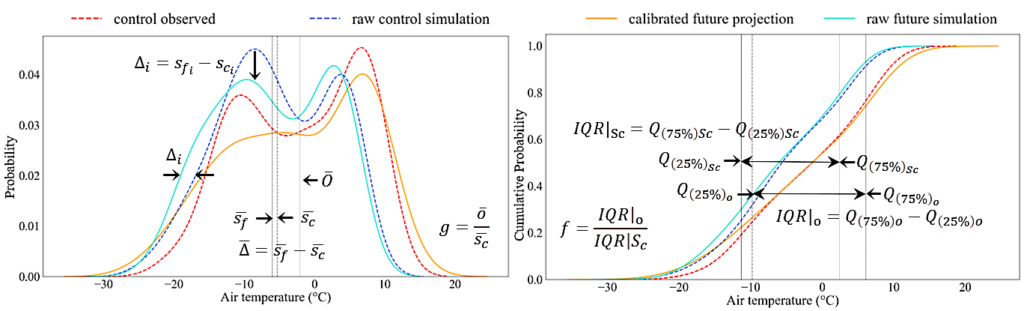
Q-Q方法使用一个函数来表示观测值和模拟值分布之间的差异规律，通过在预测时期内应用该函数，改善预测期模拟值的偏差。函数的参数通过模拟值和观测值的分位数区间和均值进行比值计算获得。我们利用已有数据，对比验证了降尺度得到的预测值与实际观测值。同时，我们将Q-Q方法的结果与常用的Quantile-mapping（Q-M）和Delta方法进行比较。

研究发现：

• Q-Q方法对于青藏高原上气候要素逐月模拟值的降尺度具有适用性，其中气压的降尺度校正具有最高的准确性，其次为气温和相对湿度，在风速和降水上的表现相对受限。尽管对于气温的校正，比值计算出的参数会影响校正结果，总体上Q-Q方法比Q-M和Delta方法的结果更加准确。
• 对于降水，适用的分位数对为10%-90%，对于其他变量，25%-75%更为适用。对于不同站点，改变分位数对不会使结果有明显提升。
• 对于不同季节和不同空间位置，Q-Q方法的表现没有明显差异。但降尺度结果受到原始GCM质量的影响较大。通过概率密度函数和累积概率函数图可以看出，变量模拟值和实际观测值分布之间的匹配程度越好，Q-Q方法在这个变量上的表现就越好。
• 由于统计降尺度方法依赖于预测期和控制期模拟值和实际观测值之间关系规律的一致性，因此当使用Q-Q方法进行连续计算时，随着误差积累和气候变化，结果准确性有所下降。此外，当增加预测期和控制期的长度时，由于减少了迭代次数，且考虑了更多气候变化的可能信息，准确性会优于连续校正得到的结果。

该工作以“Evaluating the Applicability of a Quantile–Quantile Adjustment Approach for Downscaling Monthly GCM Projections to Site Scale over the Qinghai-Tibet Plateau”为题发表在“Atmosphere”期刊上。第一作者殷子云是实验室大三学生，通讯作者南卓铜教授。/文：殷子云；核：南卓铜

【引用】Yin, Ziyun, Zhuotong Nan*, Zetao Cao, and Guofei Zhang. 2021. “Evaluating the Applicability of a Quantile–Quantile Adjustment Approach for Downscaling Monthly GCM Projections to Site Scale over the Qinghai-Tibet Plateau” Atmosphere vol. 12, no. 9: 1170. https://doi.org/10.3390/atmos12091170

论文下载：https://www.mdpi.com/2073-4433/12/9/1170 (Open Access)

Tags: pubs